Question

What is the wavelength (angstroms) of a photon that has an energy of 4.38 x 10-18 j?

Answer 1

Answer: The relationship between energy and frequency of a photon is given by E = h*f.

E is the energy, h is planck constant and f is the frequency and f= c/λ.

But i want wavelength, so i write this equation as E= h*c/λ.

now

c=3.8
`*10^(8)`

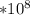
E =4.38*
`10^(-18)`
`(m^(2)*kg )/(s^(2) )`

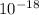
where i replaced joules for
`(m^(2)*kg )/(s^(2) )`

h = 6.62607004 *
`10^(-34)`
`(m^(2)*kg )/(s )`

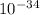
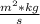
then λ = h*c/E =
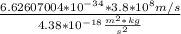`(6.62607004 *10^(-34)*3.8*10^(8)m/s)/(4.38*10^(-18) (m^(2)*kg )/(s^(2) ))` = 5.7*
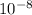`10^(-8)` m

But you want the solution in angstroms, so 1 meter is
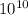`10^(10)` angstroms

so λ = 5.7*
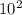`10^(2)` = 570 angstrom

Answer 2

The relationship between energy and frequency of a photon is given by

`E=hf`
where E is the energy, h is the Planck constant and f is the photon frequency. By re-arranging the equation and using the photon energy, we can calculate its frequency:

`f= (E)/(h)= (4.38 \cdot 10^(-18) J)/(6.6 \cdot 10^(-34)Js)=6.64 \cdot 10^(15) Hz`

Then we know that the photon travels at speed of light, c, so we can find its wavelength by using

`\lambda= (c)/(f)= (3 \cdot 10^8 m/s)/(6.64 \cdot 10^(15)Hz)=4.52 \cdot 10^(-8) m`

And since 1 A (angstrom) corresponds to
`10^(-15) m`, the wavelength expressed in angstroms is

`\lambda= ( 4.52 \cdot 10^(-8) m)/(10^(-15) m/A) = 4.52 \cdot 10^7 A`