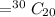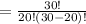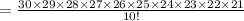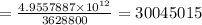Answer: Total arrangement are 30045015
Given problem will be solved with help of combination.
Explanation:
When we find the arrangement in which the order does not matter then we use combination,
Here, we have to find the possible arrangement in which order does not matter,
Thus, we will use combination to find the answer.
Here the total number of books = 30
A self contains, the number of book = 20,
Hence, the total arrangement of 20 books out of 30 books