Question

When a pendulum with a period of 2.00000 s in one location (g = 9.80 m/s2) is moved to a new location from one where the period is now 1.99863 s. what is the change in acceleration (in m/s2) due to gravity at its new location?

Answer 1

The period of a pendulum is given by:

`T=2 \pi \sqrt{ (L)/(g) }`
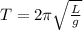
where L is the pendulum length and g is the gravitational acceleration.

Initially, the period of the pendulum is T=2.00 s while the gravitational acceleration is
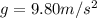
`g=9.80 m/s^2`. If we re-arrange the previous equation, we can find the pendulum length:

`L=g (T^2)/((2 \pi)^2)=(9.80 m/s^2) ((2.00s)^2)/(4 \pi^2)= 0.994 m`

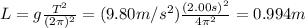
Then the same pendulum is moved to another location, and its new period is

`T=1.99863 s`. Again, by re-arranging the same equation, we can find the value of g (gravitational acceleration) at the new location:

`g=L ((2 \pi)^2)/(T^2)=(0.994 m) (4 \pi^2)/((1.99863 s)^2)=9.814 m/s^2`