Question

A survey was conducted that asked 1011 people how many books they had read in the past year. results indicated that x overbarequals14.8 books and sequals16.6 books. construct a 90​% confidence interval for the mean number of books people read. interpret the interval

Answer 1

Since we do not know the population standard deviation, we will use the t-distribution to construct the 90% confidence interval of the mean number of books people read. The value of
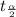
`t_{(\alpha )/(2)}` with 1010 degrees of freedom and with alpha equals to 0.10 is 1.64

First, we need to solve for the margin of error, E.

`E=t_{(\alpha )/(2)}\cdot (s)/(√(n))=1.64\cdot (16.6)/(√(1011))=0.86`

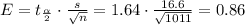
The lower bound of the confidence interval is

`LB=\overline{x}-E=14.8-0.86=13.94`

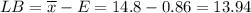
The upper bound of the confidence interval is

`LB=\overline{x}+E=14.8+0.86=15.66`

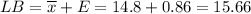
Therefore, the 90% confidence interval is (13.94, 15.66).

We are 90% confident that the interval from 13.94 books to 15.66 books does contain the true value of the population mean number of books people read.