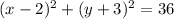Question

Can someone please help me with this? I just cannot understand this. It does not make sense to me at all. I've asked classmates, friends, teachers, and even tutors to help me but my brain just cannot comprehend this at all. Consider the following:

1. You’re baking a circular cake for a party. Your cake can be any size you want.
2. What will the radius of your cake be and how many slices will you be able to cut?
3. List the coordinates of any point in the coordinate plane.
For your original discussion post, you only need to respond to #1, #2, and #3.
View posts from your classmates and choose one to which you will respond. Answer the following questions:
1. For the cake that your classmate is baking, what would be the central angle of each slice of cake?
2. If you eat two slices of cake that are side by side, what is the measure of the arc that these two slices intercept?
3. What is the circumference of the cake?
A circle to represent the cake is graphed on the coordinate plane. What equation represents the cake if it is centered at the point that your classmate listed for #2?
This is what my classmate posted.
1. The radius of my cake is 6 inches and I can cut 8 pieces.
2. (2,-3)
Thank you so much!

Answer 1

#1: The central angle of each slice would be found by dividing the total central angle of a circle (360°) by the number of slices (8), so:


`(360)/(8) =45 $^(\circ)$`

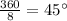Each slice would have a central angle of 45°.

#2: This question is vague, since the arc can be measured in degrees or inches. The degree measure of the intercepted arc would be 90°. The length in inches of the intercepted arc could be found using the formula:


`\frac{\text{central angle measure}}{360} *2\pi r`

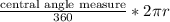
So, in your case, it'd be:


`(90)/(360) *2\pi(6)= (90)/(360) *12\pi=3\pi \text{ inches}`

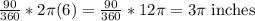
#3: The circumference of any circle is found by the equation
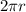
`2\pi r` wher r is the radius. So in your case it's
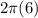
`2\pi (6)` which is
`12\pi`.

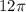
As for the equation of the circle when graphed, it's:


`(x-2)^2+(y+3)^2=36`