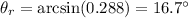Question

A ray of light passes from air into carbon disulfide (n = 1.63) at an angle of 28.0 degrees to the normal. what is the refracted angle?

Answer 1

We can solve the problem by using Snell's law, which states

`n_i \sin \theta_i = n_r \sin \theta_r`
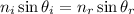
where

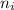
`n_i` is the refractive index of the first medium

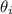
`\theta_i` is the angle of incidence

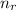
`n_r` is the refractive index of the second medium

`\theta_r` is the angle of refraction

In our problem,
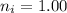
`n_i=1.00` (refractive index of air),
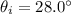
`\theta_i = 28.0^(\circ)` and
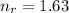
`n_r=1.63` (refractive index of carbon disulfide), therefore we can re-arrange the previous equation to calculate the angle of refraction:

`\sin \theta_r = (n_i)/(n_r) \sin \theta_r = (1.00)/(1.63) \sin 28.0^(\circ) = 0.288`
From which we find

`\theta_r = \arcsin (0.288)=16.7^(\circ)`