Question

Simplify
cosx ( tanx+cotx)

Answer 1

The first step to solving this is to use tan(t) =
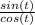
`(sin(t))/(cos(t))` to transform this expression.
cos(x) ×
`( (sin(x))/(cos(x)) + cot(x) )`
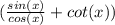
Using cot(t) =
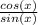
`(cos(x))/(sin(x))`,, transform the expression again.
cos(x) ×
`( (sin(x))/(cos(x)) + (cos(x))/(sin(x)) )`
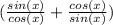
Next you need to write all numerators above the least common denominator (cos(x)sin(x)).
cos(x) ×
`(sin(x)^(2) + cos(x)^(2) )/(cos(x)sin(x))`
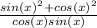
Using sin(t)² + cos(t)² = 1,, simplify the expression.
cos(x) ×
`(1)/(cos(x)sin(x))`
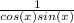
Reduce the expression with cos(x).

`(1)/(sin(x))`
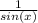
Lastly,, use
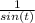
`(1)/(sin(t))` = csc(t) to transform the expression and find your final answer.
csc(x)
This means that the final answer to this expression is csc(x).
Let me know if you have any further questions.
:)