Question

The vertex form of h(x) = x2 – 14x + 6 is h(x) = (x – )2 – .

Answer 1

The vertex form of h(x) = x2 – 14x + 6 is h(x) = (x –7 )2 – 43.

Answer 2

`h(x)=(x-7)^(2) -43`

Explanation:

The given function is

`h(x)=x^(2)-14x+6`

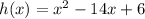
The vertex form is obtained by "completing the square". First, we have to add and subtract a term, which is formed by the squared power of half the coefficient of the linear term:

`x^(2)-14x+6\\x^(2)-14x+6+((14)/(2) )^(2)-((14)/(2) )^(2)\\x^(2) -14x+6+7^(2)-7^(2)\\x^(2) -14x+7^(2) +6-7^(2)\\(x-7)^(2) +6-7^(2) =(x-7)^(2) +6-49\\(x-7)^(2) -43`

Therefore, the expression would be
`h(x)=(x-7)^(2) -43`