For the first question, the region is a bit ambiguous.

and

intersect three times, and there are two regions between them. So either you're approximating
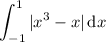
or
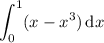
I'll assume the second case. Split the interval into 4 smaller ones, taking
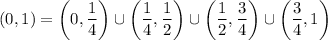
with respective midpoints of
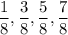
. The length of each interval is

. Note that I'm also assuming you are supposed to use equally spaced intervals.
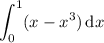
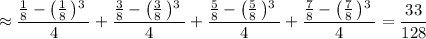
Skipping the second one since I already answered it.
For the third, split up the region of integration at some arbitrary constant

between
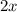
and
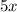
, then differentiate and apply the fundamental theorem of calculus.
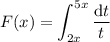
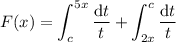
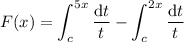
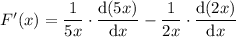

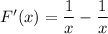
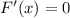
Since
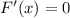
, it follows that
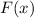
is constant.