Question

What is the area of triangle LMN

Answer 1

Area of triangle = 1/2 x base x height

Area of the triangle = 1/2 x 4 x 6 = 12 square units

Answer: 12 square units

Answer 2

A. 12 square units.

Explanation:

We have been given graph of a triangle and we are asked to find the area of our given triangle.

Since we know that area of a triangle is half the product of height of triangle and base of the triangle.

`\text{Area of triangle}=(1)/(2)*\text{Base*Height}`

We can see that MN is base of our triangle and LM is height of triangle, so let us find lengths of MN and LM using distance formula.

`\text{Distance}=√((x_2-x_1)^2+(y_2-y_1)^2)`

`\text{Distance between point M and N}=√((3--1)^2+(-4--4)^2)`

`\text{Distance between point M and N}=√((3+1)^2+(-4+4)^2)`

`\text{Distance between point M and N}=√((4)^2+(0)^2)`

`\text{Distance between point M and N}=4`

`\text{Distance between point L and M}=√((-1--1)^2+(-4-2)^2)`

`\text{Distance between point L and M}=√((-1+1)^2+(-6)^2)`

`\text{Distance between point L and M}=√(0+36)`

`\text{Distance between point L and M}=6`

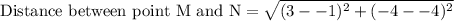
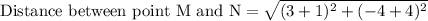
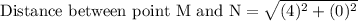
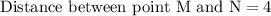
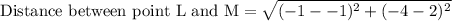
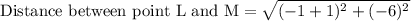
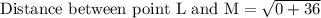
Now let us substitute our side lengths is area formula.

`\text{Area of triangle LMN}=(1)/(2)*4*6`

`\text{Area of triangle LMN}=2*6`

`\text{Area of triangle LMN}=12`

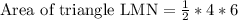
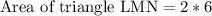
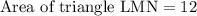
Therefore, area of triangle LMN is 12 square units and option A is the correct choice.