Question

The graph of the function y=tan(x) was horizontally stretched so that its period became 10 pi. Which is the equation of the transformed function?

Answer 1

A

Explanation:

Answer 2

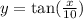`y=\tan((x)/(10))` is the equation of transformed function.

Explanation:

The graph of the function y=tan(x) was horizontally stretched so that its period became 10π

First we draw the graph of y=tan(x)

Period of tan(x) is π

We need to change period of y π to 10π by horizontal stretch.

Therefore, y=tan(ax)

where, a is horizontal stretch.

Period of y=tan(ax) is 10π

When function change y=tan(x) to y=tan(ax)

Period change π to
`(\pi)/(a)`

`(\pi)/(a)=10\pi`

`a=(1)/(10)`

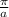
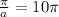
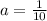
New function after horizontally stretched by factor of 10 would be
`y=\tan((x)/(10))`

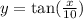
Please see the attachment of graph and horizontal stretch.

Thus,
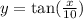`y=\tan((x)/(10))` is the equation of transformed function.