Question

An arrow is shot vertically upward from a platform 33ft high at a rate of 214ft/sec. when will the arrow hit the ground? use the formula: h=−16t2+v0t+h0. (round your answer to the nearest tenth.)

Answer 1

Hello!

Answer:

The arrow will hit the floor in 13,5 seconds.

Step-by-step explanation:

For this exercise, we have a quadratic equation that is the way (for this exercise) to calculate the time when the arrow will hit the floor, it means that the h (y) will be 0.

We have the following equation:


`h=-16 t^(2) +Vo.t+h0`

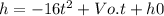
This is a quadratic equation, so we are going to use the next formula:


`\frac{-b+- \sqrt{ b^(2)-(4).(a).(c} }{2.(a)}`

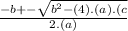
Substituting we have:


`\frac{-214+- \sqrt{ 214^(2)-(4).(-16).(33)} }{2.(-16)}`


`(-214+- √( 45796+2212) )/((-32))=(-214+- √(48008) )/((-32)) \\ =(-214+-219,10 )/((-32))`

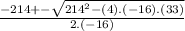
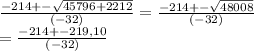
We have 2 different results, we are looking for a positive result because we are calculating a time value.

Then:


`t1=13,52s \\ t2=-0,17s`

So, we are choosing t1 because it's the positive result.

Finally, we have that the arrow will hit the floor in 13,5 seconds approximately.

Have a great day!