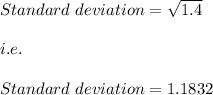Answer:
Hence, the sample standard deviation is:
1.1832
Explanation:
The data is given by:
8, 8, 8, 5, 9, 8, 7, 6, 6, 7, 7, 7, 7, 9, 9.
The mean of these data points is given by:
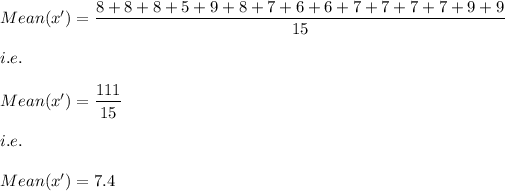
Now,
x x-x' (x-x')²
8 8-7.4=0.6 0.36
8 8-7.4=0.6 0.36
8 8-7.4=0.6 0.36
5 5-7.4= -2.4 5.76
9 9-7.4=1.6 2.56
8 8-7.4=0.6 0.36
7 7-7.4= -0.4 0.16
6 6-7.4= -1.4 1.96
6 6-7.4= -1.4 1.96
7 7-7.4= -0.4 0.16
7 7-7.4= -0.4 0.16
7 7-7.4= -0.4 0.16
7 7-7.4= -0.4 0.16
9 9-7.4=1.6 2.56
9 9-7.4=1.6 2.56
∑(x-x')²=19.69
Now the variance of the sample population is given by:
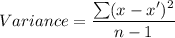
where n is the number of data points.
Here n= 15
Hence, n-1=14
Hence, we get:
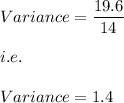
We know that the standard deviation is the square root of the variance.
i.e.