Question

Jamal states that ax + b = a(x + c), given a, b, and c are not equal to 0.

What must be the value of c for Jamal’s statement to be true?

Answer 1

`c=(b)/(a)`

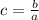
Explanation:

We have been given an equation
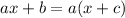`ax+b=a(x+c)`, given that a, b and c are not equal to 0.

Let us solve for the value of c that will make Jamal's statement true.

Upon dividing both sides of our equation by a we will get,

`(ax+b)/(a)=(a(x+c))/(a)`

`(ax+b)/(a)=x+c`

`(ax)/(a)+(b)/(a)=x+c`

`x+(b)/(a)=x+c`

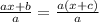
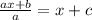
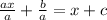
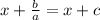
Now, we will subtract x from both sides of our equation.

`x-x+(b)/(a)=x-x+c`

`(b)/(a)=c`

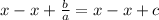
Therefore, the value of
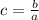`c=(b)/(a)` will make Jamal’s statement true.

Answer 2

To answer the question, we must find c of the equation:
ax + b = a (x + c)
If we divide by "a" on both sides we have to:
x + b / a = x + c
For values of "a" other than zero.
So:
c = b / a.
So that the affirmation of Jamal Be true c = b / a