Question

What is the true solution to 3 in 2 + in 8 = 2 in (4x)

Answer 1

b

Explanation:

Answer 2

The first step for solving this equation is to determine the defined range.
3㏑(2) + ㏑(8) = 2㏑(4x), x > 0
Write the number 8 in exponential form.
3㏑(2) + ㏑(2³) = 2㏑(4x)
Using ㏑(
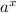
`a^(x)`) = x × ㏑(a),, transform the expression.
3㏑(2) + 3㏑(2) = 2㏑(4x)
Now collect the like terms on the left side of the equation.
6㏑(2) = 2㏑(4x)
Switch the sides of the equation.
2㏑(4x) = 6㏑(2)
Using x × ㏑(a) = ㏑(
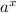
`a^(x)`),, transform the expression on the left side of the equation.
㏑((4x)²) = 6㏑(2)
Using x × ㏑(a) = ㏑(
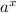
`a^(x)`),, transform the expression on the right side of the equation.
㏑((4x)²) = ㏑(
`2^(6)`)
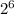
Since the bases of the logarithms are the same,, you need to set the arguments equal.
(4x)² =
`2^(6)`
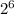
Take the square root of both sides of the equation and remember to use both the positive and negative roots.
4x = +/- 8
Now separate the equation into 2 possible cases.
4x = 8
4x = -8
Solve the top equation for x.
x = 2
Solve the bottom equation for x.
x = 2
, x > 0
x = -2
Lastly,, check if the solution is in the defined range to find your final answer.
x = 2
This means that the correct answer to your question is x = 2.
Let me know if you have any further questions
:)