Question

PLZ HELP ASAP FEATURES OF A CIRLE FROM EXPANDED EQUATION

Answer 1

First we need to convert the given equation to standard form, only then we can find the center and radius of the circle.


`x^(2) + y^(2) +18x+14y+105=0 \\ \\ x^(2) +18x+ y^(2)+14y=-105 \\ \\ x^(2) +2(x)(9)+ y^(2)+2(y)(7)=-105 \\ \\ x^(2) +2(x)(9)+ 9^(2) + [y^(2)+2(y)(7)+7^(2)] =-105+9^(2)+7^(2) \\ \\ (x+9)^(2)+ (y+7)^(2)=25`

The standard equation of circle is:


`(x-a)^(2) + (y-b)^(2)= r^(2)`

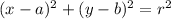
with center (a,b) and radius = r

Comparing our equation to above equation, we can write

Center of circle is (-9, -7) and radius of the given circle is 5