Question

Using the quadratic formula to solve 7x^2-x=7, what are the values of x?

Answer 1

Quadratic equation is
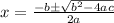
`x= \frac{-b {\pm} \sqrt{ b^(2)-4ac}}{2a}` WHEN

`a x^(2) +bx+c=0`

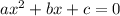
So, to make this true subtract 7 from each side.

The equation is now 7
`x^(2)` - x - 7 = 0

Values for a, b, and c: a = 7, b = -1, c = -7

Plug these variables into the quadratic equation.


`x= \frac{1 {\pm} \sqrt{ -1^(2)-4*7*-7}}{2*-7}`

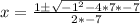
Square -1 to get 1 and multiply -4 x 7 x -7 to get 196.


`x= \frac{1 {\pm} √(1+196)}{2*-7}`

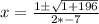
Multiply 2 x -7 to get -14, the denominator, and add 1 to 196.


`x= \frac{1 {\pm} √(197)}{-14}`

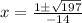
Since 197 is not a square number, and I don't know if you want to leave it in radical form or not, I will just because it's easier to understand.

Hope this helps!