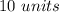2 Answers

Edyn · Answer 1 · 2019-02-16T07:31:25+0000

see the attached figure with letters to better understand the problem

Step 1

Find the length of BD

we know that

In the right triangle ABD

BD=AD ------> because is a
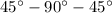$45\°-90\°-45\°$ triangle

so

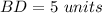
$BD=5\ units$

Step 2

Find the length of BC

In the right triangle BCD

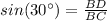
$sin(30\°)=(BD)/(BC)$

we have

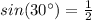
$sin(30\°)=(1)/(2)$

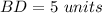
$BD=5\ units$

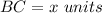
$BC=x\ units$

substitute the values and solve for x

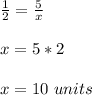
$(1)/(2)=(5)/(x)\\ \\x=5*2 \\ \\x=10\ units$

therefore

the answer is

The length of x is
$10\ units$

Please log in or register to add a comment.