Question

Setup the limit definition of definite integrals?

Answer 1

So you just need to set up the limit definition.

You would need to use the formula

`\displaystyle \int_(-1)^2(1+x^2)\mathrm dx = \lim_(n\to\infty)\sum_(i=1)^n f(x_i)\Delta x`

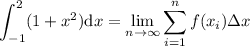
Where
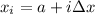
`x_i = a + i\Delta x` and
`\Delta x = \frac{b-a}n`.

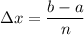
Basically we would have approximate area with
`n` rectangles with width
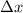
`\Delta x` and height
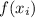
`f(x_i)`, and we have the value of n approaches to infinity.

Now, from the definite integral, we have
`a = -1, b = 2, f(x) = 1 + x^2`.

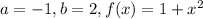
So then that would be

`\displaystyle \int_(-1)^2(1+x^2)\mathrm dx = \lim_(n\to\infty)\sum_(i=1)^n f(x_i)\Delta x \\= \lim_(n\to\infty)\sum_(i=1)^n (1+x_i^2)\frac{2 --1}n \\= \lim_(n\to\infty)\sum_(i=1)^n \left(1+\left(-1 + \frac3ni\right)^2\right)\frac{3}n`

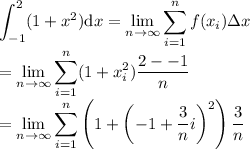
So this is how you set up the limit definition of definite integrals.

Hope this helps.