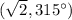Question

Which set of polar coordinates describes the same location as the rectangular coordinates (1,-1)

A. (-1, 135 degrees)
B. (sqrt 2, 315 degrees)
C. (1, 45 degrees)
D. (sqrt 2, 225 degrees)

Answer 1

The answer to this question is B. (sqrt 2, 315 degrees). This polar coordinate is the only coordinate with its angle in quadrant 4 and a length of √1^2 + (-1)^2 = √2.

Answer 2

The polar coordinate is
`(√(2),315^\circ)`

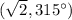
B is correct

Explanation:

Given:

Rectangular coordinates: (1,-1)

We need to change into polar coordinate.

Cartesian to polar change rule:

`(x,y)\rightarrow (r,\theta)`

`x=r\cos\theta`

`y=r\sin\theta`

`\text{Where, }r=√(x^2+y^2)\text{ and }\theta=\tan^(-1)(y)/(x)`

`=r=√(1+1)=√(2)`

`√(2)\cos\theta=1`

`√(2)\sin\theta=-1`

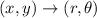
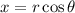
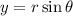
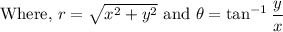
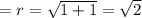
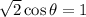
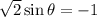
Cosine is negative and Sine is positive.

Thus, angle lie in IV quadrant.

`\theta=\tan^(-1)(-1)`

`\theta=360-45=315^\circ`

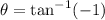
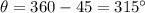
Cartesian to polar

`(1,-1)\rightarrow (√(2),315^\circ)`

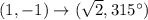
Hence, The polar coordinate is
`(√(2),315^\circ)`