Answer : Time taken for the light to reach earth is
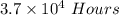
Explanation :
Given that,
Speed of Ultraviolet light,
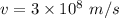
Distance covered by the light,
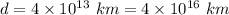
We have to find the time taken (t) by the light to reach on the surface of earth.
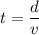
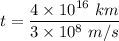
t = 133333333.333 seconds
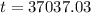
or
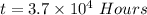
Hence, this is the required solution.