Question

A group of 15 students play different instruments, 6 play piano, 4 play violin and 5 play guitar. A student is chosen at random. What is the probability that the student chosen plays violin or piano?

Answer 1

6/15+4/15=10/15 = 2/3

Answer 2

Total number of students playing piano, violin and guitar = 15

Given: 6 students play piano, 4 play violin and 5 play guitar.

Probability of student chosen playing piano =

P(P)=
`(6)/(15)`

=
`(2)/(5)`

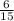
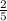
Probability of student chosen playing violin =

P(V)=
`(4)/(15)`

=
`(4)/(15)`

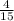
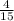
Now, we have to find the probability that the student chosen plays violin or piano.

using the formula,

`P(V\cup P)=P(V)+P(P)-P(V\cap P)`

Since there is no student chosen who plays violin and piano both, therefore
`P(V\cap P)=0`.

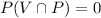Now,

`P(V\cup P)=P(V)+P(P)-P(V\cap P)`

`P(V\cup P)=(4)/(15)+(2)/(5)-0`

`P(V\cup P)=(4)/(15)+(2)/(5)`

`P(V\cup P)=(4+6)/(15)`

`P(V\cup P)=(10)/(15)`

`P(V\cup P)= 0.666`

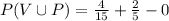
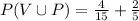
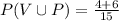
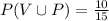
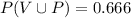
= 0.67

Therefore, the probability that the student chosen plays violin or piano is 0.67.