
Here's the solution ~
Figure 1 :
Centre (A) = (0 , 0)
let's use distance formula to find the Radius (AB) :
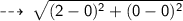
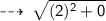
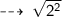
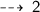
Radius = 2 units
Figure 2 :
Centre (A)= (2 , 1)
Let's solve for radius (AB) :
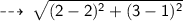
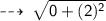
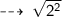
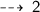
Radius = 2 units
Figure 3 :
Centre = (0 , -2)
now, let's find the Radius (AB) :
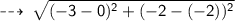
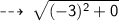
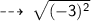
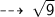

Radius = 3 units