Line segment TV has endpoints at (2,10) and (18,-18). What is the approximate length of the segment?

Question

asked Apr 19, 2019 201k views

2 Answers

Daniel Camarda · Answer 1 · 2019-04-26T10:56:00+0000

Since, a line segment TV has endpoints at (2,10) and (18,-18).

We have to determine the length of this line segment.

We will use distance formula for finding this length, which states:

For given points
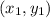and

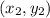
Distance(Length) =
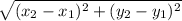
$\sqrt{(x_(2)-x_(1))^(2)+(y_(2)-y_(1))^(2)}$

So, length of line segment TV

= (2, 10) and (18,-18)

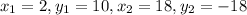
x_(1)=2 , y_(1)=10 , x_(2)=18 ,y_(2)= -18

Length of TV =
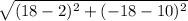
$\sqrt{(18-2)^(2)+(-18-10)^(2)}$

=
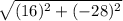
$\sqrt{(16)^(2)+(-28)^(2)}$

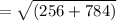
=√((256+784))

=
√(1040)

= 32.249 units

= 32.25 units

So, the length of the line segment TV is 32.25 units.