Question

One-hour carbon monoxide concentrations in 43 air samples from a section of a city showed an average of 11.6 ppm and a standard deviation of 7.08. after a traffic control strategy was put into place, 19 air samples showed an average carbon monoxide concentration of 6.4 ppm and a standard deviation of 6.94. it is known that carbon monoxide concentrations are normally distributed. the state will adopt the traffic control strategy on a large scale if there is evidence that it reduces carbon monoxide concentrations by at least 2 ppm. with h_0:\mu_1-\mu_2=2; \ \ \ h_a:\mu_1-\mu_2>2 h 0 : μ 1 − μ 2 = 2 ; h

a.μ 1 − μ 2 > 2 the appropriate test statistic is . at the 10% level of significance, we , which means that .

Answer 1

The test statistic for difference between two means is given by:


`z= \frac{(\bar{x}_1-\bar{x}_2)-(\mu_1-\mu_2)}{ \sqrt{ (\sigma^2_1)/(n_1) +(\sigma^2_2)/(n_2)} }`

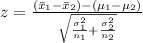
Thus, the appropriate test statistic is given by:


`z= \frac{(11.6-6.4)-2}{ \sqrt{ ((7.08)^2)/(43) +((6.94)^2)/(19)} } \\ \\ = \frac{5.2-2}{ \sqrt{ (50.1264)/(43) + (48.1636)/(19) } } = (3.2)/( √(1.1657+2.5349) ) \\ \\ = (3.2)/( √(3.7007) ) = (3.2)/(1.9237) =1.66`

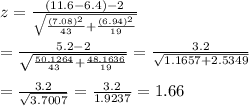
At 10% level of significance, the rejection region is given by


`z\geq z_0`

where:
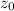
`z_0` for 10% level of significance is 1.65

Since z = 1.66 >
`z_0=1.65`, we reject the null hypothesis, which means that the traffic control strategy does not reduce carbon monoxide concentrations by at least 2 ppm.