Question

Please help with this problem see image

Answer 1

Since we have 3 sides but no angles, or known as a SSS problem, we cannot use the Law of Sines, which requires 1 angle.
Therefore we must resort to the Law of Cosines, which states:

`{c}^(2) = {a}^(2) + {b}^(2) - (2ab \cos(C)`
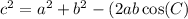
let's make <F = C, therefore c is opposite C and = 5 yd we'll make a = 6 yd and b = 7 yd
So now let's plug in and solve for Cos(C):

`{c}^(2) = {a}^(2) + {b}^(2) - (2ab \cos(C)) \\ - 2ab \cos(C) = {c}^(2) - {a}^(2) - {b}^(2) \\ - 2ab \cos(C) / - 2ab \\ = ({c}^(2) - {a}^(2) - {b}^(2)) / - 2ab`

`\cos(C) = \frac{{c}^(2) - {a}^(2) - {b}^(2)}{- 2ab} = \frac{{5}^(2) - {6}^(2) - {7}^(2)}{- 2(6)(7)} \\ = (25 - 36 - 49)/(- 2(42)) = = \frac{{5}^(2) - {6}^(2) - {7}^(2)}{- 84}`

`\cos(C)= ( - 60)/( - 84) = (5)/(7) \\ C = { \cos((5)/(7) ) }^( - 1) = 44.42 \: degrees`
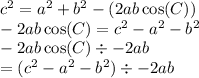
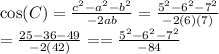
Therefore the answer is A) 44° !!

Answer 2

Using Cosine Rule:

5² = 7² + 6² - 2(7)(6) cos(F)

25 = 85 - 84cos(F)

84 cos(F) = 60

cos(F) = 5/7

F = cos⁻¹(5/7)

F = 44°

Answer: 44°