Question

What is m ∠DEC if measure of Arc DC = 150° and measure of Arc AB = 90°?

A. 150°
B. 120°
C. 240°
D. 90°

Answer 1

B.
`120^(\circ)`

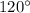
Explanation:

We have been given an image of a circle. We are asked to find the measure of angle DEC.

Upon looking at our given circle, we can see that angle DEC is formed by the intersection of secants AC and BD inside the given circle.

We know that intersecting secants theorem states that angle formed by two secants inside the circle is half the sum of intercepted arcs.

Using intersecting secants theorem, we can set an equation as:

`m\angle DEC=\frac{\text{Measure of arc AB+ Measure of arc DC}}{2}`

`m\angle DEC=(150^(\circ)+90^(\circ))/(2)`

`m\angle DEC=(240^(\circ))/(2)`

`m\angle DEC=120^(\circ)`

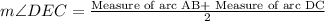
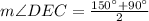
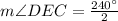
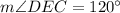
Therefore, measure of angle DEC is 120 degrees and option B is the correct choice.

Answer 2

we know that
Inner angle, has its center at an inner point of the circle.
The measure of the interior angle is the half-summit of the arcs that comprise it and its opposite.
so
m ∠DEC=[Arc DC+Arc AB]/2------> [150+90]/2-----> 120°

the answer is
120°