Question

What is the measure of ∠K, to the nearest degree?

13
24
66
72

Answer 1

66is my first choice answer

Answer 2

In the given triangle, we have to find the measure of
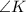`\angle K` to the nearest degree.

By applying law of sine which states

"In a triangle ABC, with angles A, B and C and side opposite angle A is 'a', side opposite to angle B is 'b' and side opposite to angle C is 'c'. Therefore, the sine law is:

`(\sin A)/(a)=(\sin B)/(b)=(\sin C)/(c)`

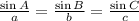
Now, applying law of sine in the triangle JLK,
`\angle L=76^(\circ) , l=53, k=50`

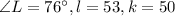
Therefore,
`(\sin J)/(j)=(\sin K)/(k)=(\sin L)/(l)`

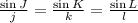
Using the ratio,
`(\sin K)/(k)=(\sin L)/(l)`

`(\sin K)/(50)=(\sin 76)/(53)`

`\sin K=(\sin 76 * 50^(\circ))/(53)`

`\sin K=0.915`

`\angle K=\arcsin 0.915`

`\angle K= 66.2`

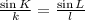
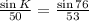
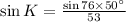
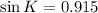
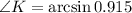
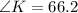
Therefore,
`\angle K= 66^(\circ)`

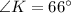
Therefore, Option 3 is the correct answer.