Question

Tricia Measured the snow falling and Ledge on her window. In 30 minutes the snow increase from 1/4 inch to 3/4 of an inch. By how many did the snow increase?

A) 1 inch
B) 1/4 inch
C)1/2 inch
D)3/8 inch

Answer 1

Hello!

To find the increase in depth, we must subtract the initial depth from the final depth. This can can be represented by the following formula:

(change in depth) = (final depth) – (initial depth)

Insert any known values into the equation above and simplify:

(change in depth) =
`(3)/(4)` –
`(1)/(4)`
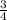
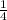
change in depth =
`(2)/(4)`

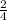
We have now proven the change in depth to equal
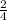
`(2)/(4)`. We know, however, that this fraction can be reduced to a value of
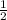
`(1)/(2)`. Therefore, the answer to this problem is C.

I hope this helps!

Answer 2

C, because of 1/2 = 2/4. 2/4 plus 1/4 equals 3/4.