Answer: The correct options are (A) up and (A) 2 units to the left of the function g(x)
Step-by-step explanation: We are given the following functions:
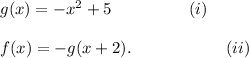
We know that the vertex form of a function h(x) is
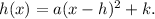
The function h(x) opens down if a < 0 and opens up if a > 0.
Substituting the value of g(x) from equation (i) in (ii), we have
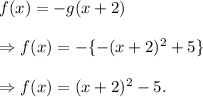
Comparing it with the vertex form, we get
a = 1 > 0.
So, f(x) opens up.
Also, the value of 'x' co-ordinate in f(x) is increased by 2 units as compared to g(x), so the graph of g(x) is shifted horizontally 2 units to the left of the function g(x).
The graphs of both the functions f(x) and g(x) are attached below.
Thus, the graph of function f(x) opens (A). up
and
the graph of the function f(x) is shifted horizontally (A). 2 units to the left of the function g(x).