Answer:
A. Cosine is the correct answer
Explanation:
We are given the figure having an right triangle with acute angle 48° and the hypotenuse 170 feet.
Since, we know,
The trigonometric forms are given by,
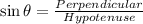
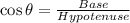
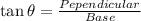
As, we are given the length of the hypotenuse and are required to find the length of the base.
We will have to use the cosine formula.
That is,
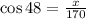
Hence, option A is correct.