Question

PLZ HELP ASAP DIVIDE LINE SEGMENTS

Answer 1

A (4,8) and b (7,2) and let c (x,y)

A , B and C are col-linear ⇒⇒⇒ ∴ slope of AB = slope of BC
slope of AB = (2-8)/(7-4) = -2
slope of BC = (y-2)/(x-7)
∴ (y-2)/(x-7) = -2
∴ (y-2) = -2 (x-7) ⇒⇒⇒ equation (1)

The distance between two points (x₁,y₁),(x₂,y₂) = d

`d = \sqrt{ (x2-x1)^(2) + (y2-y1)^(2) }`

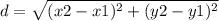
The ratio of AB : BC = 3:2
AB/BC = 3/2
∴ 2 AB = 3 BC

`2 * \sqrt{ (7-4)^(2) + (2-8)^(2) }` =
`3* \sqrt{ (x-7)^(2) +(y-2)^(2) }`
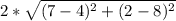
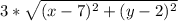
eliminating the roots by squaring the two side and simplifying the equation
∴ 4 * 45 = (x-7)² + (y-2)² ⇒⇒⇒ equation (2)
substitute by (y-2) from equation (1) at equation (2)
4 * 45 = 5 (x-7)²
solve for x
∴ x = 9 or x = 5
∴ y = -2 or y = 6

The point will be (9,-2) or (5,6)
the point (5,6) will be rejected because it is between A and B

So, the point C = (9,-2)

See the attached figure for more explanations