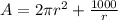Question

A closed can, in a shape of a circular, is to contain 500cm^3 of liquid when full. The cylinder, radius r cm and height h cm, is. made from thin sheet metal. The total external surface area of the cylinder is A cm^2.

Show that A=2πr^2 + 1000/r.

Answer 1

To express the height as a function of the volume and the radius, we are going to use the volume formula for a cylinder:
`V= \pi r^2h`
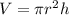
where

`V` is the volume

`r` is the radius

`h` is the height

We know for our problem that the cylindrical can is to contain 500cm^3 when full, so the volume of our cylinder is 500cm^3. In other words:
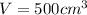
`V=500cm^3`. We also know that the radius is r cm and height is h cm, so
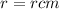
`r=rcm` and
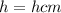
`h=hcm`. Lets replace the values in our formula:

`V= \pi r^2h`

`500cm^3= \pi (rcm^2)(hcm)`

`500cm^3=h \pi r^2cm^3`

`h= (500cm^3)/( \pi r^2cm^3)`

`h= (500)/( \pi r^2)`

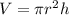
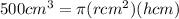
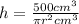
Next, we are going to use the formula for the area of a cylinder:
`A=2 \pi rh+2 \pi r^2`
where

`A` is the area

`r` is the radius

`h` is the height

We know from our previous calculation that
`h= (500)/( \pi r^2)`, so lets replace that value in our area formula:

`A=2 \pi rh+2 \pi r^2`

`A=2 \pi r((500)/( \pi r^2))+2 \pi r^2`

`A= (1000)/(r) +2 \pi r^2`
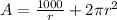
By the commutative property of addition, we can conclude that:

`A=2 \pi r^2+(1000)/(r)`