Question

During the first part of a​ trip, a canoeist travels 18 miles at a certain speed. the canoeist travels 4 miles on the second part of the trip at a speed 5 mph slower. the total time for the trip is 3 hrs. what was the speed on each part of the​ trip?

Answer 1

We can set it up like this, where s is the speed of the canoeist:


`(18)/(s) + (4)/(s-5) = 3`

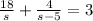
To make a common denominator between the fractions, we can multiply the whole equation by s(s-5):


`s(s-5)[(18)/(s) + (4)/(s-5) = 3] \\ 18(s-5)+4s=3s(s-5) \\ 18s - 90+4s=3 s^(2) -15s`

If we rearrange this, we can turn it into a quadratic equation and factor:


`18s - 90+4s=3 s^(2) -15s \\ 22s-90=3 s^(2) -15s \\ 3 s^(2) -37s+90=0 \\ (3s-10)(s-9)=0 \\ s= (10)/(3) ,9`

Technically, either of these solutions would work when plugged into the original equation, but I would use the second solution because it's a little "neater." We have the speed for the first part of the trip (9 mph); now we just need to subtract 5mph to get the speed for the second part of the trip.


`9-5 = 4`

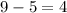
The canoeist's speed on the first part of the trip was 9mph, and their speed on the second part was 4mph.