Question

What happens to the value of the expression n+15 as n decreases?

Answer 1

Hello!

As the variable n decreases in size, the value of the given expression will decrease in size as well.

For example, let's say that n=22. When you add 22 to 15, you'll get 37 as your answer. Let's say that n decreases by 1 every time you use it in the given expression. Now n=21. When 21 is added to 15, your answer is 36. As you can see, the value of the expression had decreased as the value of n decreased.

I hope this helps! :)

Answer 2

If n decreases to one or zero, the expression will converge to 16 or 15, but if n decreases to minus infinity, the expression will diverge to minus infinity. The diference between the value of the expression, and the value of n, is always 15.

Explanation:

To explain this result, we have to treat the expression as a succession, which we can write as

`a_(n)=n+15`

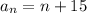
then, to analyze it, we have to know which type of number is n (but the problem doesn't tell us).

In mathematics, in general, n is used to name a natural number (this is, n=1, 2, 3, 4, ...), but sometimes n is a natural number plus zero (this means n=0, 1, 2, 3, ...). Nevertheless, in this problem it is not said which type of number n is, therefore it could be an integer too (this means n=..., -2, -1, 0, 1, 2, ...). And we will stop there and not say that n could be real, fractional, irreal, etc. (which could be, as it is not defined in the problem).

Therefore, as n is decreasing, we will take the limit of n decreasing to its three possible versions:

`\lim_(n \to \ 1) a_n=1+15=16; n \in \mathbb{N}`

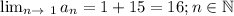
if n is natural,

`\lim_(n \to \ 0) a_n=0+15=15; n \in \mathbb{N}_0}`

if n is natural plus zero, and

`\lim_(n \to -\infty) a_n=-\infty+15=-\infty; n \in \mathbb{Z}`

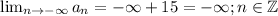
if n is an integer.

So, these are the correct answers to the general expression given in the problem.