Question

A circle is centered at (−4, 9) and has a radius of 11.

What is the equation of the circle?

Enter the equation in the box using lower case variables x and y.


_____________________

Answer 1

`\bf \textit{equation of a circle}\\\\ (x- h)^2+(y- k)^2= r^2 \qquad center~~(\stackrel{-4}{ h},\stackrel{9}{ k})\qquad \qquad radius=\stackrel{11}{ r} \\\\\\\ [x-(-4)]^2+[y-9]=11^2\implies (x+4)^2+(y-9)^2=121`

Answer 2

The equation of the circle is
`(x+4)^2+(y-9)^2=121`.

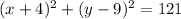Explanation:

The standard form of a circle is

`(x-h)^2+(y-k)^2=r^2`

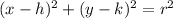
where, (h,k) is the center of the circle and r is the radius.

It is given that the circle is centered at (−4, 9) and has a radius of 11.

Substitute h=-4, k=9 and r=11 in the above equation.

`(x-(-4))^2+(y-9)^2=(11)^2`

`(x+4)^2+(y-9)^2=121`

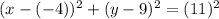
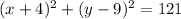
Therefore the equation of the circle is
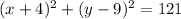`(x+4)^2+(y-9)^2=121`.