For the solution/answer of this question, we will use the double angle formula which can be derived as follows:
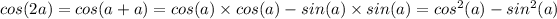
Now, the above expression can be simplified to:
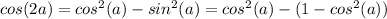 (Because
(Because
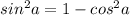 )
)
Therefore, we can further simplify it to:
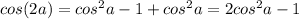 which is the proof which is required.
which is the proof which is required.
Thus, we have proved that:
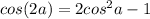
Thus, this equality is true for all values of a.