Solve for x ~ x {}^(2) - 7x + 12 = 0 thankyou ~​

Question

Solve for x ~

`x {}^(2) - 7x + 12 = 0`

thankyou ~​

Answer 1

x = 3,4

Explanation:

`\displaystyle \large{(x-a)(x-b)=x^2-bx-ax+ab \longrightarrow x^2-(b+a)x+ab}`

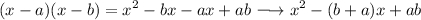
Above is formula for factoring of two brackets for a = 1 from ax^2 + bx + c.

First, find the factors of 12:

• 1 and 12
• 2 and 6
• 3 and 4

If we multiply the factors together, we get same ab-value which is 12. Next, we find the middle term. A middle term can’t be found by adding factors together.

Our middle term is -7x and the only factors that satisfy -7x would be 3 and r using (x-a)(x-b) standard.

Hence, our a is 3 and b is 4. Substitute in:

`x^2-7x+12 = x^2-(3+4)x + 3(4) = (x-3)(x-4)`

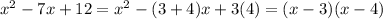
Set (x-3)(x-4) = 0 then we obtain:

x-3 = 0 or x-4 = 0 —> solve like linear by transporting the constant and change the sign.

Hence, “x = 3 or x = 4”

You can also write x = 3,4 instead or x = 4,3.

Answer 2

`\qquad \qquad\huge \sf༆ Answer ༄`

let's solve ~

`\qquad \sf \dashrightarrow \: {x}^(2) - 7x + 12 = 0`

`\qquad \sf \dashrightarrow \: x {}^(2) - 4x - 3x + 12 = 0`

`\qquad \sf \dashrightarrow \: x(x - 4) - 3(x - 4) = 0`

`\qquad \sf \dashrightarrow \: (x - 4)(x - 3) = 0`

Therefore, the required values of x are ~

`\overbrace{  \underbrace{\underline{ \boxed{ \sf 3 \: and \: 4}}}}`