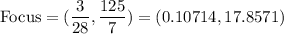Question

The equation of a parabola is given.

y=14x2−3x+18



What are the coordinates of the focus of the parabola?


Enter your answer in the boxes.

Answer 1

The answer is (6, 10)

Also, you might want to make sure you include the division line in 1/4 because 1/4 and 14 result in very different answers, thus the insane answer that someone else gave you!

Answer 2

The coordinates of the focus of the parabola is:

`\text{Focus}=((3)/(28),(125)/(7))=(0.10714,17.8571)`

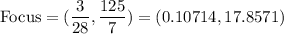
Explanation:

We know that for any general equation of the parabola of the type:

`(x-h)^2=4p(y-k)`

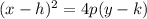
The focus of the parabola is given by:

Focus= (h,k+p)

Here we are given a equation of the parabola as:

`y=14x^2-3x+18`

On changing the equation to general form as follows:

`y=14(x^2-(3)/(14)x)+18\\\\\\y=14((x-(3)/(28))^2-((3)/(28))^2)+18\\\\y=14(x-(3)/(28))^2-(9)/(56)+18\\\\\\y=14(x-(3)/(28))^2+(999)/(56)\\\\y-(999)/(56)=14(x-(3)/(28))^2\\\\(x-(3)/(28))^2=(1)/(14)(y-(999)/(56))\\\\(x-(3)/(28))^2=4* (1)/(56)(y-(999)/(56))`

Hence, we have:

`h=(3)/(28)\ ,\ k=(999)/(56)\ ,\ p=(1)/(56)`

Hence,

`k+p=(1000)/(56)=(125)/(7)`

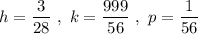
Hence, focus is:

`\text{Focus}=((3)/(28),(125)/(7))=(0.10714,17.8571)`