\sqrt[3]{ \sqrt[3]{2} - 1} = \sqrt[3]{a} + \sqrt[3]{b} + \sqrt[3]{ (1)/(9) } \\ \\ If \: a>b \: \: , \: \: Find \: \: (a+2b) \:.

Question

`\sqrt[3]{ \sqrt[3]{2} - 1} = \sqrt[3]{a} + \sqrt[3]{b} + \sqrt[3]{ (1)/(9) } \\ \\ If \: a>b \: \: , \: \: Find \: \: (a+2b) \:.`

Answer 1

Define

`c=\sqrt[3]{\sqrt[3]{2}-1}-\sqrt[3]{(1)/(9)} \approx 0.157435964092`

Then you have the symmetrical equation

`c=\sqrt[3]{a}+\sqrt[3]{b}`
which can be solved for b to give

`b=(c-\sqrt[3]{a})^(3)`

Substituting into your expression gives

`a+2b=a+2(c-\sqrt[3]{a})^(3)`

The requirement that a > b means this is only relevant for

`a > ((c)/(2))^(3) \approx 0.000487777605001`

The attached graphs show the general shape of a+2b and some detail near the origin. "a" is plotted on the x-axis; "b" is plotted on the y-axis.

Answer 2

Step One
Subtract cube root 1/9 to the left hand side. Or subtract cube root (1/9) from both sides.

`\sqrt[3]{ \sqrt[3]{2} -1 } - \sqrt[3]{ (1)/(9) } = \sqrt[3]{a} + \sqrt[3]{b}`

Step Two.
There is a minus sign in front of
`{-}\sqrt[3]{ (1)/(9) }`
We must get rid of it. Because it is a minus in front of a cube root, we can bring it inside the cube root sign like so, and make it a plus out side the cube root sign

`{+}\sqrt[3]{ (-1)/(9) }`

Step Three
Write the Left side with the minus sign placed in the proper place

`\sqrt[3]{ \sqrt[3]{2} -1 } + \sqrt[3]{ (-1)/(9) } = \sqrt[3]{a} + \sqrt[3]{b}`

Step Four
Equate cube root b with cube root (-1/9)

`\sqrt[3]{b} = \sqrt[3]{ (-1)/(9) }`

Step Five
Equate the cube root of a with what's left over on the left

`\sqrt[3]{ \sqrt[3]{2} -1 } = \sqrt[3]{a}`

Step 6.
I'll just work with b for a moment.
Cube both sides of cube root (b) = cube root (-1/9)

`\sqrt[3]{b} ^(3) =\sqrt[3]{ (-1)/(9) }^3}`

`\text{b =} (-1)/(9)`

`\text{2b =}(-2)/(9)`

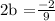Step seven
the other part is done exactly the same way
a = cuberoot(2) - 1.

What you do from here is up to you. It is not pleasant.
Is this clearer?

a + 2b should come to cuberoot(2) - 1 - 2/9
a + 2b should come to cuberoot(2) - 11/9

I hope a person is marking this. I wonder how many of your class mates got it.