The expression given to us is:
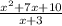
This can be rewritten as:
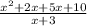
Now, let us take
 as the common factor in the first two terms in the numerator and 5 as the common factor in the last two terms in the numerator. Thus, we get:
as the common factor in the first two terms in the numerator and 5 as the common factor in the last two terms in the numerator. Thus, we get:
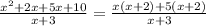
Now, taking
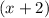 as the common factor, we get:
as the common factor, we get:
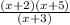
The above is the simplest form of the given expression,
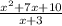
As we know that the denominator of a rational expression can never be zero, thus the only restriction in our case will be:
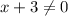
or,
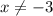 (subtracting 3 from both sides)
(subtracting 3 from both sides)
Thus, the restriction is that
 cannot be equal to
cannot be equal to
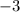 .
.