Question

A person is standing exactly 36 ft from a telephone pole. there is a 30° angle of elevation from the ground to the top of the pole. what is the height of the pole? 12 ft ft 18 ft ft

Answer 1

B

Explanation:

heart

Answer 2

As per the statement:

A person is standing exactly 36 ft from a telephone pole. there is a 30° angle of elevation from the ground to the top of the pole.

⇒Distance of a person from the telephone pole = 36 ft.

and angle of elevation (
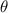`\theta`) = 30 degree.

We have to find the height of the pole.

Let h be the height of the pole.

Using tangent ratio:

`\tan \theta = \frac{\text{opposite side}}{\text{adjacent side}}`

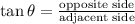
Here,

Opposite side = h foot

Adjacent side = 36 ft

Angle of elevation:
`\theta = 30^(\circ)`

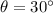
Substitute these to solve for AB:

`\tan 30^(\circ) = (h)/(36)`

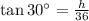
or

`h = 36\cdot \tan 30^(\circ)`

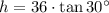
or

`h = 36\cdot (1)/(√(3))`

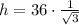
Simplify:

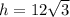`h = 12√(3)` ft

Therefore, the height of the pole is
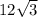`12√(3)` ft