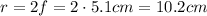Question

An object is placed 18 cm in front of spherical mirror.if the image is formed at 4cm to the right of the mirror, calculate it's focal length. Is the mirror convex or concave? What is the nature of the image? What is the radius of curvature of the mirror

Answer 1

1) Focal length

We can find the focal length of the mirror by using the mirror equation:

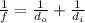
`(1)/(f)= (1)/(d_o)+ (1)/(d_i)` (1)
where
f is the focal length

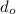
`d_o` is the distance of the object from the mirror

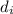
`d_i` is the distance of the image from the mirror

In this case,
`d_o = 18 cm`, while
`d_i=-4 cm` (the distance of the image should be taken as negative, because the image is to the right (behind) of the mirror, so it is virtual). If we use these data inside (1), we find the focal length of the mirror:

`(1)/(f)= (1)/(18 cm)- (1)/(4 cm)=- (7)/(36 cm)`
from which we find

`f=- (36)/(7) cm=-5.1 cm`

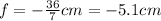
2) The mirror is convex: in fact, for the sign convention, a concave mirror has positive focal length while a convex mirror has negative focal length. In this case, the focal length is negative, so the mirror is convex.

3) The image is virtual, because it is behind the mirror and in fact we have taken its distance from the mirror as negative.

4) The radius of curvature of a mirror is twice its focal length, so for the mirror in our problem the radius of curvature is:

`r=2f=2 \cdot 5.1 cm=10.2 cm`