Question

Jacob has some cookies. 3/4 of his cookies are chocolate chip. Out of the chocolate chip cookies 1/8 of them have nuts as well. What fraction of Jacobs cookies are chocolate chip cookies with nuts?

Answer 1

The answer is: "
`(1)/(6)` " .
_______________________________________________________
Step-by-step explanation:
________________________________________________________
Given the fractions:

"3/4" ; and "1/8" ;

Note the "denominators: "4" and "8" .

We can easily convert "3/4" to its fraction value with a denominator of "8" ;

→ "3/4" = " (what value?) / 8" ?

→ Look at the "denominators" :

→ 4 * (what value?) = "8" ? ; → "8 ÷ 4 = "2" ;

→ So, 4 * 2 = 8 ; for the "denominator" ; so we multiply by "2" in the
"numerator" , as well:

→ "(3/4)" = (3*2)/(4*2) = "6/8" ;
__________________________________________________
→ "3/4" = "6/8" ;
__________________________________________________
→ Note: The entire batch of cookies is: "8/8" ; or "1 whole" ;
{since: "8/8" = "{8÷8 = 1 whole}" ;
__________________________________________________

Given: "3/4" of the {entire batch of} his cookies are chocolate chip." ;

i.e. "6/8 out of 8/8" are chocolate chips ;

6/8 are chocolate chips;

1/8 out of 6/8 are {"chocolate chip with nuts"} ;
______________________________________________
==> What fraction of cookies are {"chocolate chip with nuts"} ?
__________________________________________________

To get the answer; we simplify: "1/8 out of 6/8";

or, simplify, "1/8 out of 3/4" ;

that is:

"
`(1)/(8)` ÷
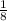
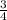
`(3)/(4)` " = ? {our answer} ?? ;

→ "
`(1)/(8)` ÷
`(3)/(4)` " ;

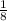
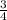
→ Note: When we divide 2 (TWO) fractions; we find the equivalent by writing the expression with a multiplication sign; AND by "inverting" (or taking the "reciprocal" of) the "second" fraction ;

= "
`(1)/(8)` *
`(4)/(3)` " ;
_______________________________________________________

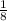
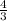
Note: The "4" cancels out to a "1" ; and the "8" cancels out to a "2" ;

since: "{8 ÷ 4 = 2}" ; and since: "{4 ÷ 4 = 1 }" ,
________________________________________________________
And we can rewrite the expression as:
________________________________________________________

→ "
`(1)/(2)` *
`(1)/(3)` " ;

And simplify further:

= "
`((1*1))/((2*3))` ;

= "
`(1)/(6)` " .
______________________________________________________

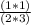
The answer is: "
`(1)/(6)` " .

______________________________________________________
Variant: At the point {above} which we have:
______________________________________________________

→ "
`(1)/(8)` *
`(4)/(3)` " ;
______________________________________________________
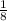
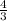
Simplify further; as following:

= "
`((1*4))/((8*3))` ;

= "
`(4)/(24)` " ;

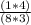
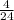
= " (4 ÷ 4) / (24 ÷ 4) " ;

= "
`(1)/(6)` " .

_______________________________________________________

The answer is: "
`(1)/(6)` " .
_______________________________________________________

Answer 2

Well, we can find the answer by multiplying the two fractions. 3/4*1/8 equals 3/32.