Question

In the figure below, lines that appear to be tangent are tangent. Point O is the center of the circle. Which of the following is the value of x ?

-60
-90
-100
-120

Answer 1

D. 120
360-(90+90+60)=120

Answer 2

For a better understanding of the solution provided here please go through the diagram in the file attached.

There are atleast two ways to solve this question. We will use the "Outside Angle Theorem" which states that "The measure of an angle formed by two secants, two tangents, or a secant and a tangent from a point outside the circle is half the difference of the measures of the intercepted arcs."

We will apply this theorem to our question and we get the following equation:

Thus,

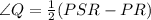`\angle Q=(1)/(2)(\overarc{PSR}- \overarc{PR})`..........(Equation 1)

Now, we know that if the measure of arc PR is
`x^(\circ)` then the measure of arc PSR has to be
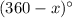`(360-x)^(\circ)`. And we already know that
`\angle Q=60^(\circ)`.

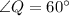Thus, substituting these values in (Equation 1) we can easily calculate the value of the unknown
`x^(\circ)` as:

`60^(\circ)=(1)/(2)(360^(\circ)-x^(\circ)-x^(\circ))`

`360^(\circ)-2x^(\circ)=2* 60^(\circ)=120^(\circ)`

`2* x^(\circ)=360^(\circ)-120^(\circ)=240^(\circ)`

`\therefore x=120^(\circ)`

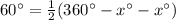
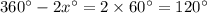
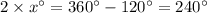
Thus the last option is the correct option.