Question

Factor completely: 9x3 + 9x2y - 4x - 4y

Answer 1

`9x^3 + 9x^2y - 4x - 4y`


`= 9x^2(x + y) -4(x + y)`


`= (x +y)(9x^2-4)`


`= (x +y)(3x - 2)(3x + 2)`

Answer 2

`(x+y)(3x+2)(3x-2)`

Explanation:

The given expression is
`9x^3+9x^2y-4x-4y`

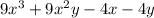
Make group as shown below

`(9x^3+9x^2y)+(-4x-4y)`

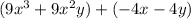
Factor out GCF from each of the group

`9x^2(x+y)-4(x+y)`

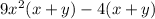
Now, factored out the common term

`(x+y)(9x^2-4)`

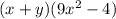
Now, rewrite the expression in perfect square form

`(x+y)((3x)^2-2^2)`

Apply the difference of squares formula:
`a^2-b^2=(a+b)(a-b)`

`(x+y)(3x+2)(3x-2)`

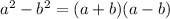
Hence, the factored form of the given expression is

`(x+y)(3x+2)(3x-2)`