The slope would always be the coefficient of x, so in this case, we can already rule out A and B. C and D are left now.
Since the line passes through the point (4,-1), let's sub in x = 4 (since the x value is 4), and if we get y = -1, the answer can be determined.
Option C:
y =

x -
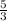
Sub x = 4,
y =

(4) -
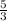
= 1
The answer was NOT y = -1, so we can rule out C.
That leaves us with the only option D, and just to check in case:
y =

=

= -1
D is definitely the answer! Hope this helped!