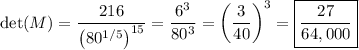Quick warning that this is not the most elegant solution.
Let
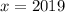 and
and
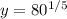 , so the matrix whose determinant we want looks like this:
, so the matrix whose determinant we want looks like this:
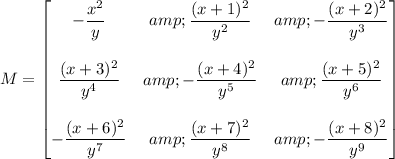
Since it's a 3x3 matrix, we can just compute the determinant directly using a Laplace expansion. Along the first row, for instance, we get

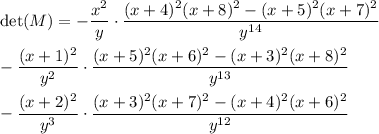
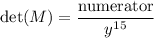
where the numerator is
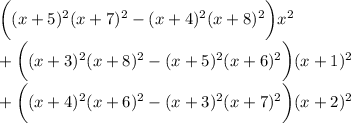
Now just simplify. The numerator reduces drastically to a constant, 216. Then