Question

What is the length of AB¯¯¯¯¯, to the nearest tenth of a centimeter?

angle A = 42 Angle c = 50 Triangle ABC BC = 12

Answer 1

AB = 13.7 cm.

We will use the law of sines to solve this:
sin A/a = sin B/b = sin C/c

We know that BC, or side a, is 12. We know that angle A is 42, and angle C (across from AB, or side c) is 50:
(sin 42)/12 = (sin 50)/x

Cross multiply:
x*sin 42 = 12*sin 50

Divide both sides by sin 42:
(x*sin 42)/(sin 42) = (12*sin 50)/(sin 42)
x = 13.74 ≈ 13.7

Answer 2

13.7 centimeters.

Explanation:

Please find the attachment.

We have been given that angle A of triangle ABC measures 42 degrees and angle C measures 50 degrees. The length of segment BC is 12 units. We are asked to find the length of segment AB.

We will use law of sines to solve for the length of AB as shown below:

`(AB)/(sin(C))=(BC)/(sin(A))`

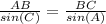
Upon substituting our given values we will get,

`(AB)/(sin(50^(\circ)))=(12)/(sin(42^(\circ)))`

`(AB)/(0.766044443119)=(12)/(0.669130606359)`

`(AB)/(0.766044443119)*0.766044443119=(12)/(0.669130606359)*0.766044443119`

`AB=17.9337185983715039*0.766044443119`

`AB=13.7380254767`

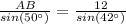
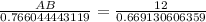
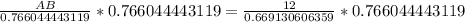
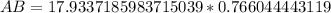
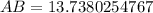
Upon rounding our answer to the nearest tenth of a centimeter we will get,

`AB\approx 13.7`

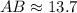
Therefore, the length of AB s 13.7 centimeters.