Question

Solve 6 over x minus 6 equals the quantity of x over x minus 6, minus six halves. for x, and determine if the solution is extraneous or not.

Answer 1

x = 6; this is an extraneous solution.

Explanation:

The equation we are given is

`(6)/(x-6)=(x)/(x-6)-(6)/(2)`

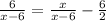
First we will simplify the constant. 6/2 = 3; this gives us

`(6)/(x-6)=(x)/(x-6)-3`

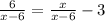
Next, we will multiply all terms by (x-6) in order to eliminate the denominator:

`(6)/(x-6)* (x-6)=(x)/(x-6)* (x-6)-3* (x-6)\\\\6=x-3(x-6)`

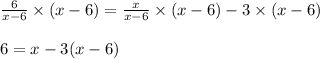
Using the distributive property, we have:

`6=x-3(x-6)\\\\6=x-3(x)-3(-6)\\\\6=x-3x--18\\\\6=x-3x+18`

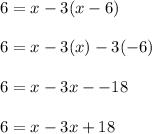
Combining like terms on the right, we have

6 = -2x + 18

Subtract 18 from each side:

6-18 = -2x+18-18

-12 = -2x

Divide both sides by -2:

-12/-2 = -2x/-2

6 = x

However, if we were to use 6 for x, this would give us 0 in the denominators; thus it is an extraneous solution.

Answer 2

6/(x - 6) = x/(x - 6) - 6/2
6/(x - 6) = x/(x - 6) - 3
6 = x - 3(x - 6)
6 = x - 3x + 18
-12 = -2x
x = 6
However, substituting x = 6 makes the denominator equal to zero, the this is an extraneous solution.